Understanding decision under constraints with triangular decisions
On Sun, 18 Jun 2023, by @lucasdicioccio, 1695 words, 0 code snippets, 8 links, 7images.
I want to start a series of articles on multi-criteria decisions. Since the topic is broad, I’d like to first write an article about decisions under constraints, starting with triangular tradeoffs.
Triangular tradeoffs
Triangular tradeoffs are tradeoffs where you lay options along the sides of a
triangle, and you can only pick one corner of the triangle, leaving the
opposite side unavailable (it also works if each corner is an option and you
need to pick one side). You can construct a triangular trade-off with the
template sentence A,B,C - pick two.
Examples of triangular tradeoffs:
- Good, Fast, Cheap – pick two
- Consistent, Available, Partition-Tolerant – pick two
- Energy, Money, Time – pick two
- Joy, Skill, Needs – pick two
You probably have encountered such sentence because triangular tradeoffs arise in many contexts. The first example is a form of #project-management gimmick. The second example is the CAP-Theorem: an impossibility result in computer science. Whereas the two last ones are motivational frameworks to help us go on with our lives.
These tradeoffs have the same structure about three competing goals that we can place on triangle sides. The next section explains how to thing about triangular tradeoffs.
modeling triangular tradeoffs
The most direct representation of triangular tradeoffs is, well, to have a triangle: annotate the sides with the criteria and the decision is which corner to pick. When picking a corner of a triangle, we actually chose an option which is explicitly characterized along two desireable criteria (e.g., Good and Cheap) while implicitly leaving out the third criteria (i.e., not Fast). Since a triangle has three corners, there are three possible choices. And we can illustrate the three possible choices in the following picture.
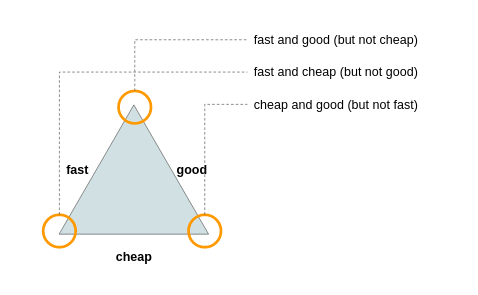
When we draw such a picture, we implicitly hide some information. In the triangle, each side represents a favorable outcome of a decision. Thus, corner encodes a combination of independant criteria. Goodness (Good or not), cost (Cheap or not), and time-to-delivery (Fast or not) are the three independant criteria.
Let’s give a numerical representation to each criteria, say 1 represents the
favorable outcome and 0 represents the unfavorable outcome. For instance, 1
is Good, and 0 is not-Good. With this simple formalims we can then use a
three-digit number like 011 to represent various positions on the triangle.
The first digit (leftmost) encodes cost, the second digit encodes goodness, and
the third digit (rightmost) encodes time-to-delivery. Thus 101 encodes
(Cheap, not-Good, Fast). We can now annotate our triangle with these numbers,
which is akin to giving a name to each corner:
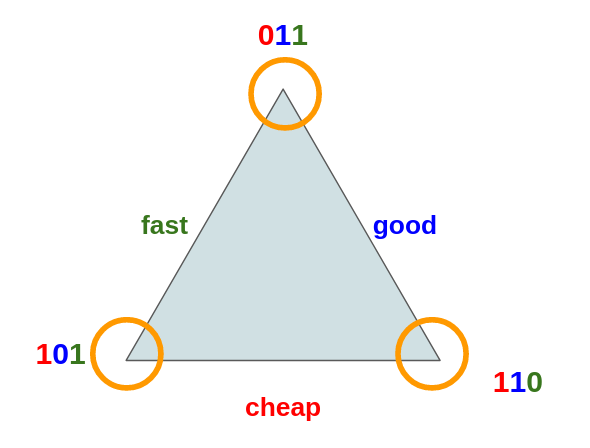
In addition to giving a name to each corner, I’ve also colored each digit and the triangle-side according to the criteria they represent. The picture carries a lot of information: we started saying there are three options to chose from (each corner) and elaborated that we also chose from three criteria (individual digits). Decisions on corners or decisions on digits are inter-related: if we pick one corner we also pick three digits, the converse is true. Thus either way of deciding leads to the same result, but these decisions are different. This story becomes confusing and we are approaching the important lesson of this article. Let’s focus now on what is the relationship between deciding on corners and deciding on digits.
corners or three-digit numbers?
In triangular decisions, there is some confusion about what we “chose”. Indeed, the decision we make when taking a corner of the triangle is related to (but different from) the decision we make when picking a single digit. Confusion arises due to the fact that, in the latter case, we are deciding under constraints. Whereas, when picking a corner, the #constraints have already been resolved.
The “pick two” of the triangular tradeoff template sentence actually is a constraint: we must pick a number so that the sum of the digits is two. In contrast, “pick a corner” is a shortcut to name configurations which happens to have two connected sides: someone (the first human who draw a triangle) already solved the problem “the sum of digits is two” and provided us with a menu of three choices.
Recapitulating: with binary values to represent each of the three possible
criteria, we have eight possible configurations. Further, we are given the
constraint “pick two”. We formalize this constraint as the sum of the digits is two. Doing so reduces the triangle tradeoff to “pick a corner” among three
configurations. When evaluating decisions
this reduction of the decision space is welcome as we a smaller decision space
facilitates the evaluation of a decision. What is important to internalize here
is that the reduction in the number of configurations is not attributed to a
“choice”, instead it is the application of constraints.
We can generalize the shortcut-trick to problems having more than three binary criteria. For instance if you are used to playing board game you already know that a tetrahedron can encode “a,b,c,d – pick three” (much like a four-sided die picks one out). Thus overall, what we want to study the general framework of applying constraints to reduce the size of a decision space.
deciding under constraints
This section elaborates the general framework of decision under constraints.
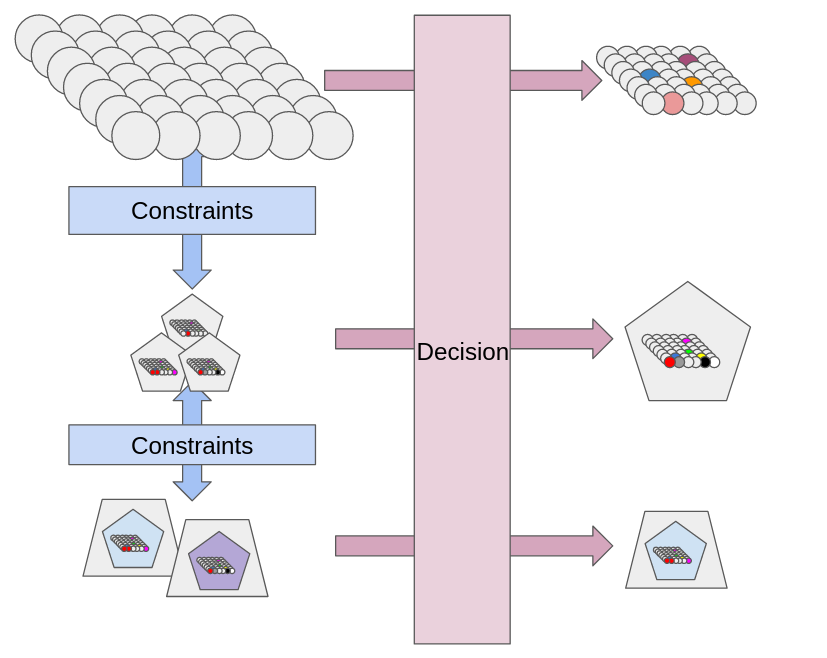
Rather than a simple triangular decision, we are given a set of atomic decisions. These are primitive decisions such as prices, delays, quality, or amounts of sugar cane. We are tasked to decide. That is, among all the possible configurations, we need to pick one configuration. Figuratively, we can represent a choice and (a subset of the possible configurations) as follows:
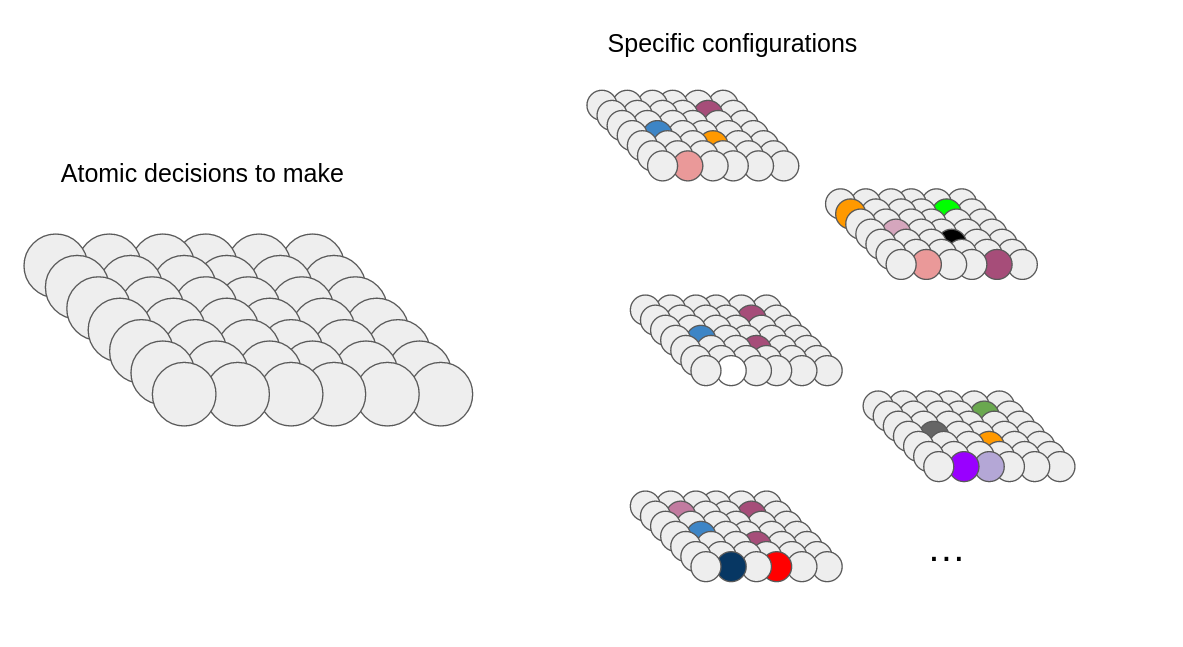
In the above picture, we lay down all the small atomic decisions we have to make in gray circles, coloring these decisions means making a choice. Once we color all the circles (which I have not done in the picture because it is fastidious), we have settled on a particular configuration.
What makes a decision difficult is pairwise. On the first hand, the number of configurations grows exponentially with the number of atomic decisions. On the other hand, evaluating each single decision can cost much effort. Some real-world rules such as physics boundaries, personal preferences, or regulations, reduce the set of decisions we can make.
As the analysis of the triangular tradeoff as shown us, we have two ways to decide:
- either we make choices about one configuration in one-fell swoop
- or we apply constraints, step back and decide on a reduced set of configurations
The following picture recapitulates these two paths. Top-left, we find our set of atomic decisions. When deciding directly (moving right) we end up with a particular configuration. Whereas we can also first apply some constraint, which means we are left to chose from a reduced set of “bundled” configurations.
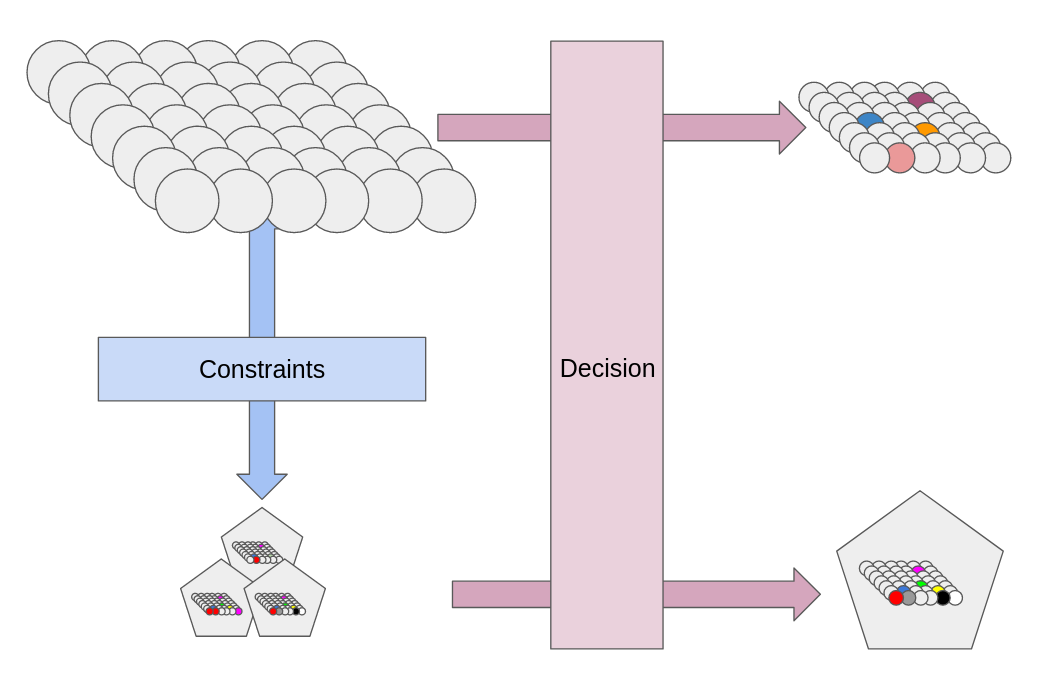
The distinction between these two decision processes is tenuous: when we decide in one-fell swoop we shall still apply the constraints to arrive to a solution. When we have many constraints, nothing prevents to repeat the process. Indeed, decisions can also take more steps. At each decision step, applying some constraints bundles some configurations from the previous decision-step.
Other decision-making processes can exist as well if we change slightly the definition of “decision”. For instance, let’s extend the “decision” step with the added power to eliminate at least one-value. That is to say, we can make the decision to do a tiny bit of progress by reducing the set of candidates. Using, this decision repeatedly betweeen applications of some constraints also drive us towards a final decision. Potentially, the final decision happens when a single configuration is left over.
Further, we could extend this process so that a decision step could influence the constraints (e.g., re-ordering them or even creating new ones). Such a technique could allow to capture secondary goals when some condition on the left over combinations happens (e.g., when two options are acceptably performant, consider some risk-threshold before making a by-cost tie-break).
We can illustrate (two steps) of such a process as follows.
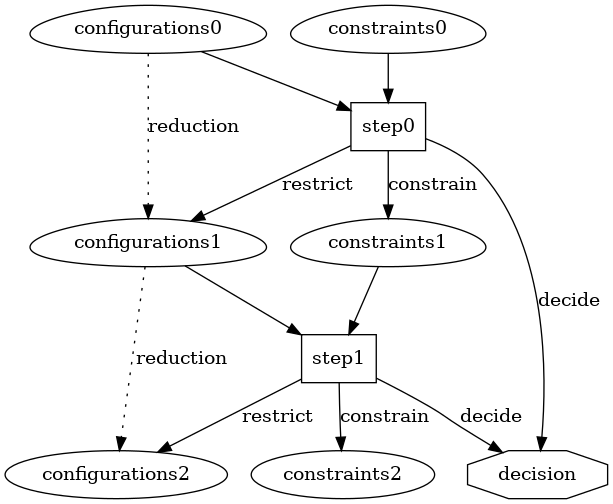
Summarizing, we’ve describes a pretty general decision-making process for decisions under constraints. This process is “recursive” (or fractal and prone to self-references if you prefer): the choice we make when pruning configuration or when picking a constraint for the next step, in itself, is a deicsion. This process is mechanical and deterministic as we can describe it with such graphs. Therefore, if our decision-making process were perfect, we should end up chosing the same configuration in either path. On the opposite, we ultimately make informed-guesses.
An #informed-guess is a nice euphemism for instinct-based decisions. There is nothing wrong with such informed-guesses. Indeed, if we annotate the picture from my article about “judging decisions, not outcomes”, we see that applying constraints to a problem will either reduce the enumeration difficulty or change the evaluation difficulty (e.g., because the constraint pruned some options which required some rare expertise before continuing).
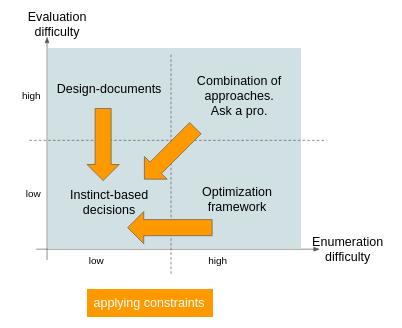
Although there is nothing wrong with an informed guess, they are easy to conflate with a rushed decision. In appearance, the shortcut we took in triangular tradeoffs is beneficial because we started from eight configurations and ended up with three configurations. We discarded some solutions subject to related constraints. For instance, admit that “pick at most two” rather than “pick exactly two” is a valid representation of our business case. We then admit more than three solutions (we now have seven solutions). Solutions under the “pick at most two” constraint could be beneficial on other factors that you have not yet accounted for. As a result people tend to challenge solutions with their own interpretation of business rules. Such disagreement can be frustrating. In short, keep in mind that the solution “neither fast, nor cheap, nor good” actually exists and someone, somewhere, may be championing this solution as an alternative to yours. My recommendation against corporate-decisions paralysis is to document decision processed (e.g., via design docs) so that constraints and evaluation criteria are spelled out.
Summary and conclusion
We discuss the process of deciding under constraints. Starting, from the example of triangular tradeoffs. Such problems asks people to make a pick among three options. These three options actually capture a configuration among three distinct binary decisions (e.g., good or bad, fast or slow, cheap or expensive). Seemingly we should have to pick among eight configurations. The difference between the two approaches to a same problem is that we applied a constraint (“pick two”) and renamed to three possible configurations.
We then generalize the constraint-application step and sketch a decision-framework of iterative changes to an initial problem. The framework is pretty general and typically the goal is to restrict the number of configurations enough that some instinct-based decision becomes possible. In corporate context, this decision-process is often split among multiple people at various hierarchical ranks.
Real-world decision-making is messy: models capture a biased and sparse vision of reality. Further, our constraint-solving ability is also imperfect: we may misrepresent constraints and economical realities binds us. Ultimately, we make informed guess. In such situation, we need to remember that the final-decision often is an instinct-based decision or frustration will prevail.